Isogeometric collocation
The most widely used approach to solve partial differential equations in computational solid mechanics is the finite element method, which is normally applied to a weak form of the PDE of interest. Finite element schemes are also referred to as variational or Galerkin methods. Collocation methods are an alternative approach in which the strong form of the partial differential equation is enforced at a set of sites called collocation points. The advantage is that collocation methods are faster than variational methods, especially when the efficiency is directly related to the cost of quadrature (e,g. in explicit structural dynamics). The needed requirement of additional smoothness has been a significant obstacle for the development of collocation methods as classical finite elements are only C0-continuous. This limitation is no longer present in isogeometric analysis, a spline-based finite element method which uses smooth basis functions. Isogeometric collocation has recently triggered a great interest, as it performs better than Galerkin in terms of accuracy per unit of computing time.
In collaborations with colleagues in Austin and Pavia, we proposed the solution to some issues related to Neumann boundary conditions for highly nonuniform meshes and developed the first frictionless contact formulation for the collocation framework, which we later extended to the frictional case also for Cosserat rods. The striking advantage of collocation for contact is that the formulation is based on a pointwise contact evaluation, similarly to the node-to-segment approach in standard finite elements, yet it passes the contact patch test to machine precision. The solution algorithm takes advantage of the two-half-pass contact strategy.
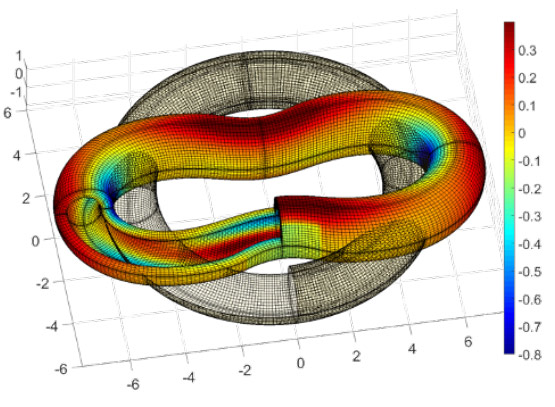
We also investigated collocation for hyperelasticity, as well as for structural mechanics, namely, for Reissner-Mindlin shells and for geometrically exact three-dimensional beams in implicit and explicit dynamics problems. Within ongoing work, we are seeking to exploit the efficiency of isogeometric collocation within the computational homogenization framework, investigating two-scale strategies with various combinations of Galerkin and collocation strategies at the micro- and macroscales to optimize computational efficiency. These approaches are applied to hyperelasticity problems in heterogeneous materials.
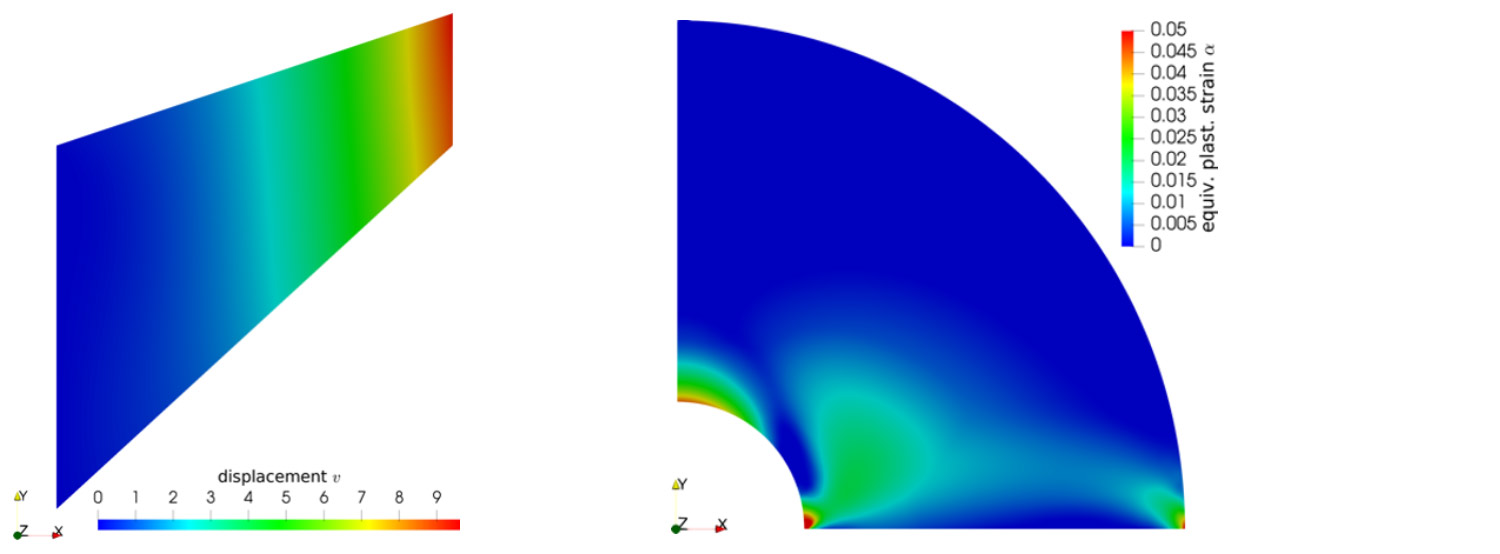
Very recently, we investigated a mixed stress-displacement isogeometric collocation approach for nearly incompressible elastic materials and for materials exhibiting von Mises plasticity. The proposed method circumvents the stability issues of the primal collocation formulation for plasticity. Volumetric locking issues could also be successfully treated.
Funding:
external page DFG external page Priority Program SPP1748 “Development of non-conventional discretization methods, mechanical and mathematical analysis” (1st phase, 2015-2017).
external page DFG International Research Training Group 1627, “Virtual materials and their validation: German-French school of computational engineering” (2015-2019).
external page DFG external page Priority Program SPP1748 “Development of non-conventional discretization methods, mechanical and mathematical analysis” (2nd phase, 2018-2020).