A bridge between collocation and Galerkin
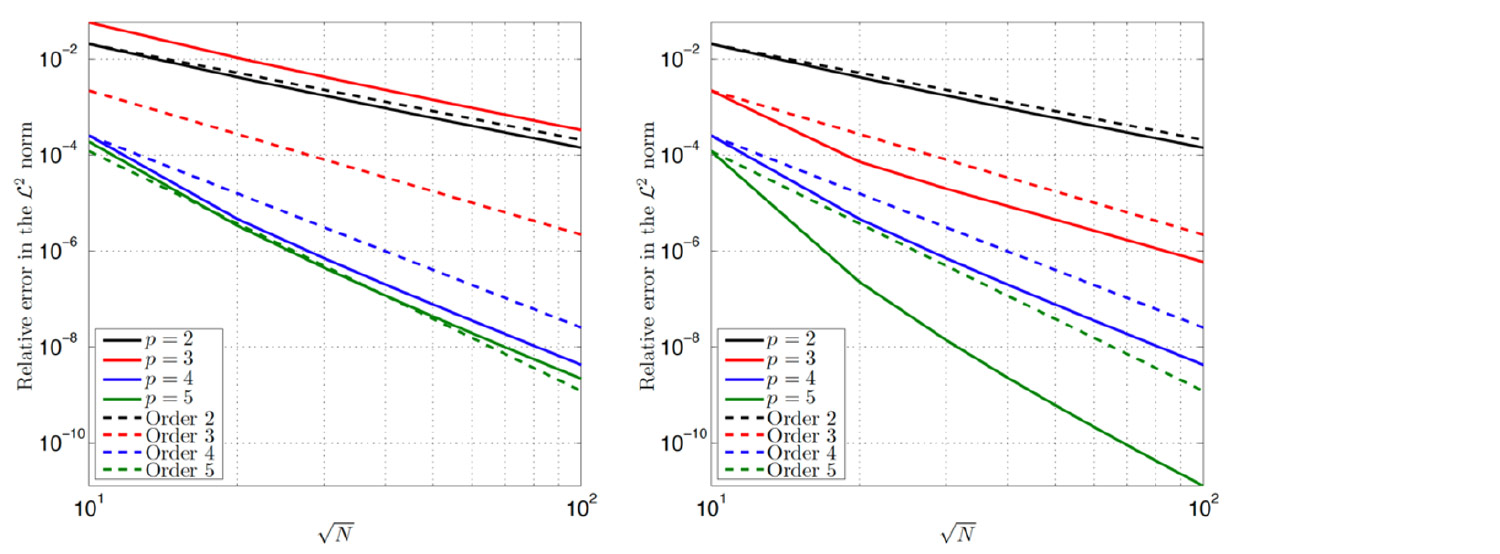
The accuracy per degree of freedom of collocation is significantly lower than that of Galerkin schemes. In particular, the order of spatial convergence for isogeometric collocation at the standard collocation points is equal to p for even and p -1 for odd degrees (p = polynomial degree). This odd/even discrepancy in the convergence order is well known since the first papers on isogeometric collocation in 2010.
Recently, we proposed the variational collocation method for the numerical solution of partial differential equations. The conceptual basis is the establishment of a direct connection between the Galerkin method and the classical collocation methods, with the perspective of achieving the accuracy of the former with the computational cost of the latter. Variational collocation requires a discrete space constructed by smooth and pointwise non-negative basis functions, which makes the approach immediately applicable to IGA and some meshfree methods. In our paper, we concentrate on IGA and demonstrate that there exists a set of points - named Cauchy-Galerkin (CG) points - such that collocation of the strong form at these points produces the Galerkin solution exactly.
Since CG points are not known a-priori, estimates are necessary in practice and can be found based on superconvergence theory. We show that applying isogeometric collocation at the estimated CG points completely solves the odd/even discrepancy in the order of spatial convergence. We demonstrate the potential of variational collocation with examples of linear and non-linear elasticity as well as Kirchhoff plates. The approach has the potential to make a significant impact in the computational mechanics community, as it can be extended to the solution of any elliptic PDE, as well as to the use of different basis functions satisfying the basic requirements of continuity and non-negativity. Another potential application of the approach is the development of new reduced quadrature schemes for IGA. For odd degrees of discretization, we obtain spatial convergence rates and accuracy very close to those of accurately integrated standard Galerkin with a quadrature rule of two points per parametric direction independently of the degree.
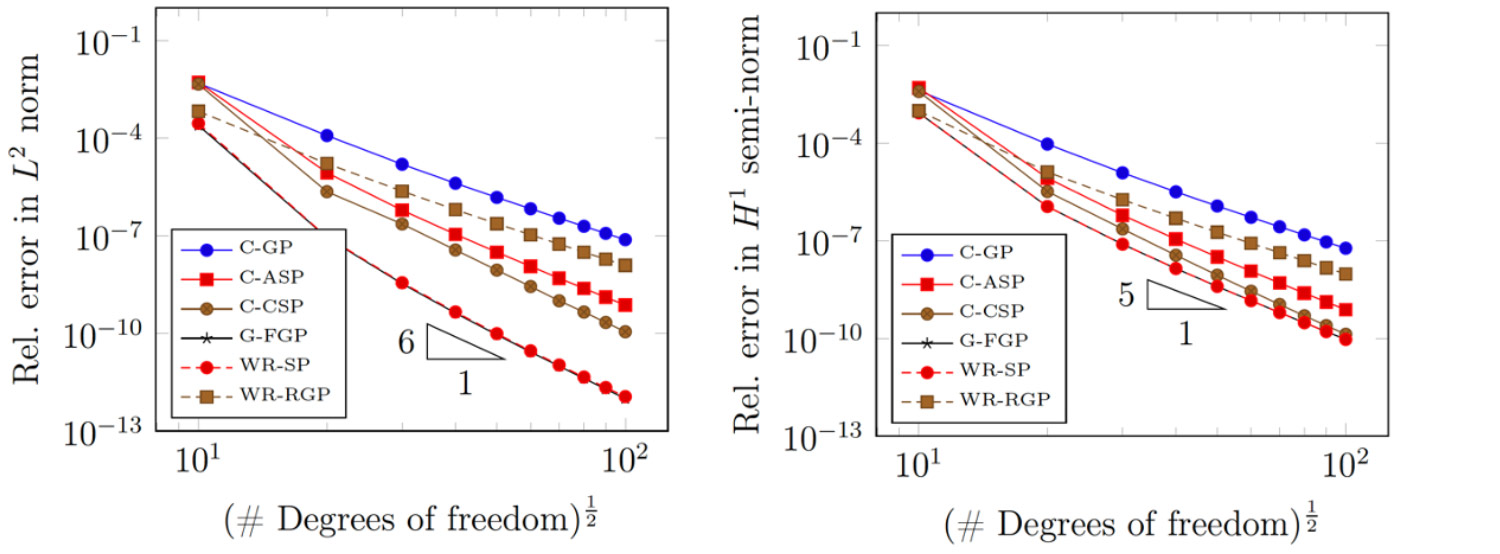
Our new reduced quadrature scheme (WR-SP) achieves an accuracy very close to the Galerkin scheme with full quadrature (G-FGP) using only 2 quadrature points per parametric direction independently of p
Funding:
external page DFG external page Priority Program SPP1748 “Development of non-conventional discretization methods, mechanical and mathematical analysis” (1st phase, 2015-2017).