Probabilistic fracture modeling

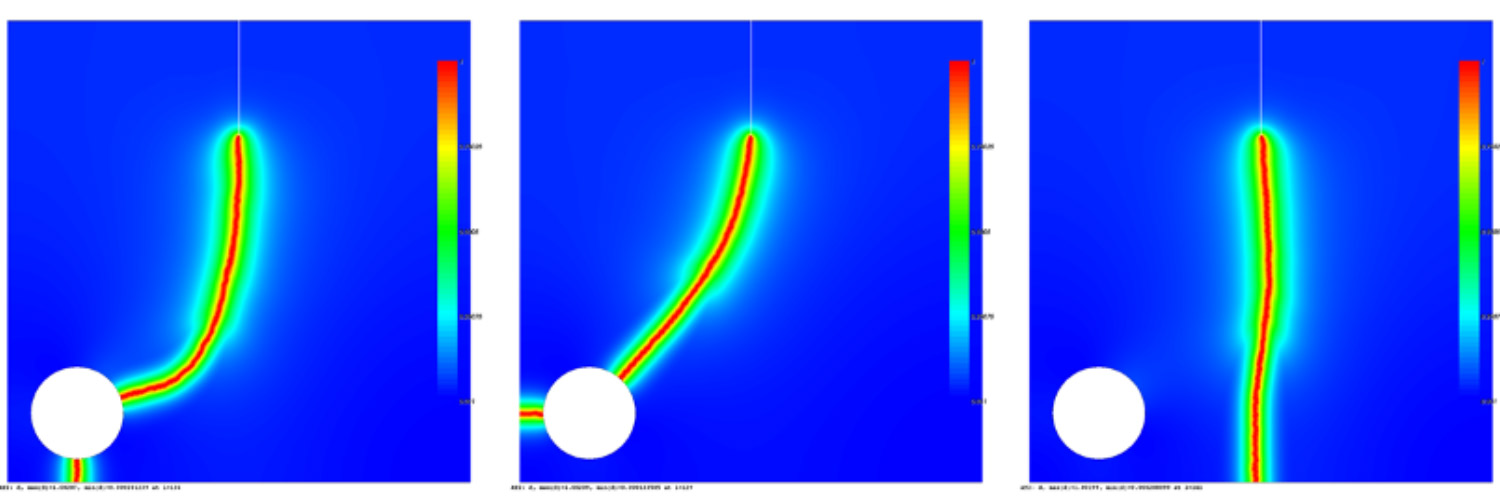
In variational phase-field modeling of brittle fracture, the functional to be minimized is not convex, so that the necessary stationarity conditions of the functional may admit multiple solutions. The solution obtained in an actual computation is typically one out of several local minimizers. Evidence of multiple solutions induced by small perturbations of numerical or physical parameters is occasionally recorded in the literature.

In this project, carried out in collaboration with our colleagues at the external page TU Braunschweig, we advocate a paradigm shift, away from the search for one particular solution towards the simultaneous description of all possible solutions (local minimizers), along with the probabilities of their occurrence. To this end, we propose the stochastic relaxation of the variational brittle fracture problem through random perturbations of the functional, giving rise to the concept of stochastic solution represented by random fields or random variables with values in the classical deterministic solution spaces.

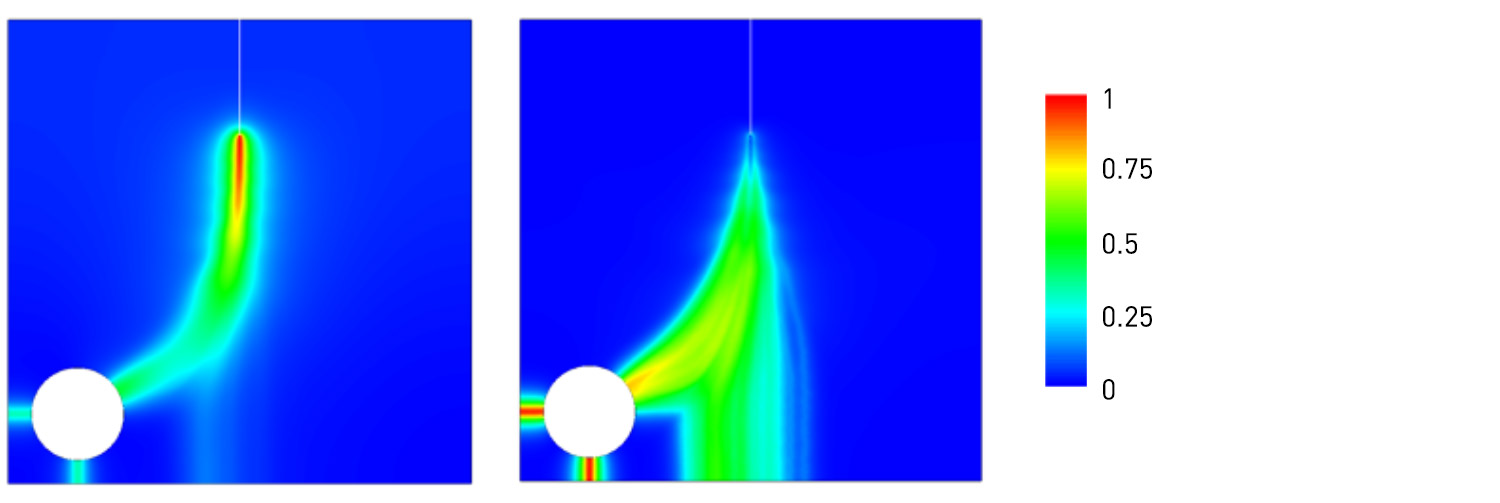
In the numerical simulations, we use a simple Monte Carlo approach to compute approximations to such stochastic solutions. The final result of the computation is not a single crack pattern, but rather several possible crack patterns and their probabilities. The stochastic solution framework using evolving random fields allows additionally the interesting possibility of conditioning the probabilities of further crack paths on intermediate crack patterns. We recently submitted a paper on the first outcomes of this project.