Fracture in porous media
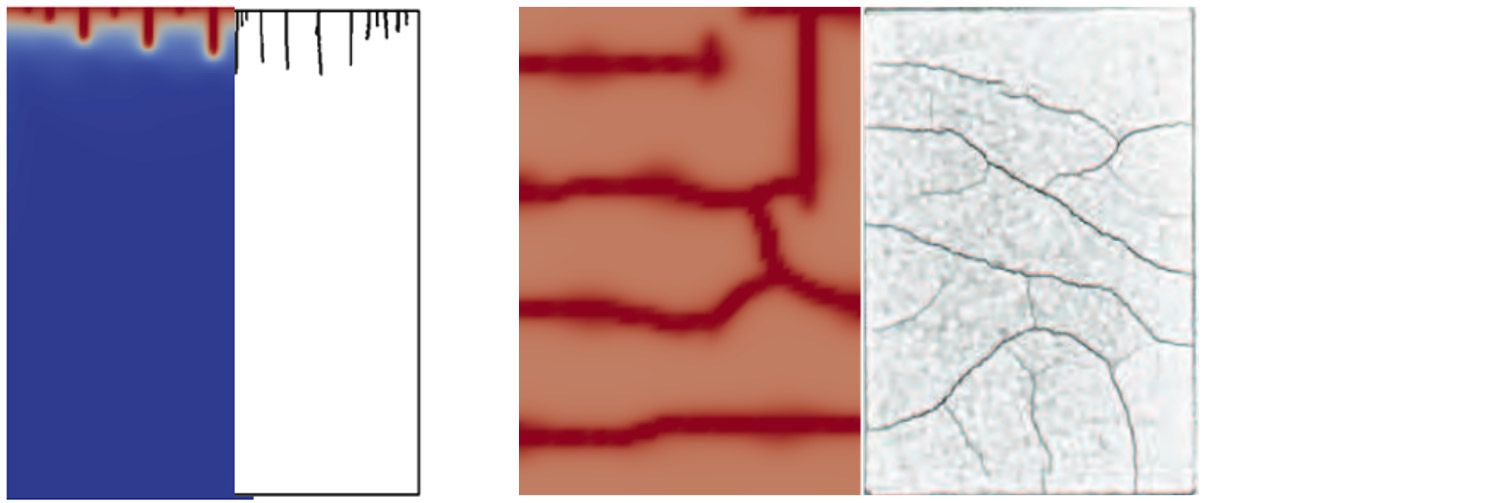
Porous media are ubiquitous in nature and technology, a few relevant examples being soils, cement-based materials, hydrogels and biomechanical tissues. These materials are constituted of a solid skeleton and pores filled with fluids like air, water or oil. Fluid transport in the pore network is coupled with the deformation of the solid skeleton. During desiccation, the loss of fluid leads to shrinkage of the material, and restrained shrinkage may lead to fracture. We developed a phase-field model to simulate desiccation-induced cracking in porous media. The modeling framework is based on the theory of variably saturated porous media, which is coupled with a phase-field model of brittle fracture using the concept of effective stress. The fracture energy of the material also varies with the water content. We first applied our model to investigate desiccation in soils and compared with experimental data from the literature. We then addressed cracking induced by drying shrinkage in cement-based materials. In collaboration with our colleagues at external page EMPA we performed experiments to deliver calibration and validation data. The numerical results showed very good agreement with the experiments.

The finite element discretization of phase-field models of fracture in porous media is prone to locking. This is due both to the hydraulic and to the mechanical properties of the material: porous media with low permeability are locally incompressible immediately after the application of a load; in phase-field models where the asymmetry in behaviour between tension and compression is recovered through a volumetric-deviatoric split of the elastic energy, the ratio between volumetric and deviatoric stiffness can become very high.
To solve these problems, we developed a mixed u-p-α (displacement - pressure - phase-field) and a mixed u-p-pw-α (displacement - pressure - fluid pressure - phase-field) formulation for phase-field modeling of fracture in elastic materials and in saturated porous media, respectively. In both cases, satisfaction of the inf-sup condition for stability prevents the use of linear interpolations for all unknown fields; on the other hand, using a quadratic interpolation for the displacements and a linear interpolation for the other unknowns is effective but leads to a very high computational cost. To solve this issue we propose a stabilization technique based on polynomial pressure projections, which leads to stable behaviour also when linear interpolations for all unknown fields are adopted.
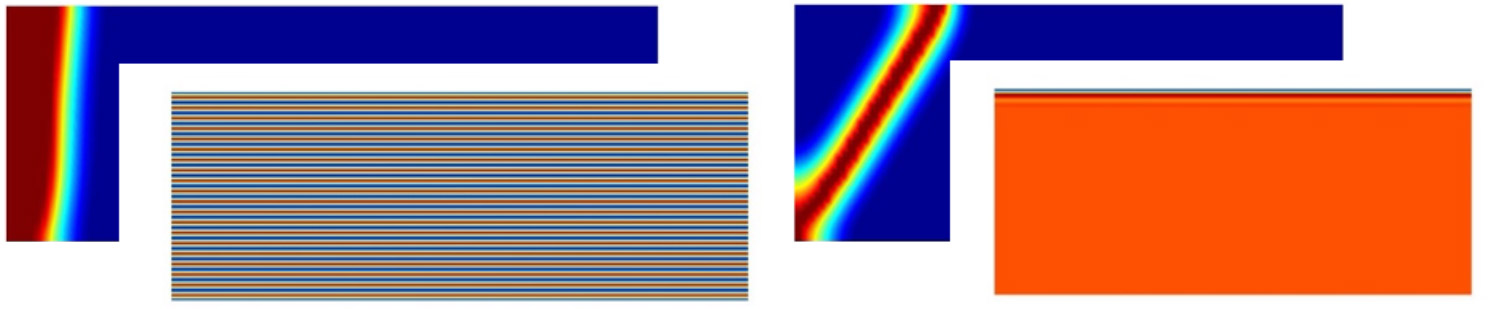
Two-dimensional shear test in a water-saturated specimen: Phase-field (upper left rectangle) and water pressure distribution (lower right rectangle) immediately after the localization of the crack. In the left figure the solution is obtained with a standard mixed formulation and linear finite elements for all unknowns (unstable). The phase-field localization band is anomalously thick and the fluid pressure distribution is oscillatory. In the right figure the solution is obtained with the proposed stabilized formulation and linear finite elements (stable). The phase-field localization band and the fluid pressure distribution are as expected.
Funding:
external page DFG external page Research Training Group 2075 “Modelling the constitutive evolution of building materials and structures with respect to aging” (2015-2019)