Phase-field modeling of ductile fracture
The first phase-field formulation for fracture was based on the assumption of brittle behavior. We were among the first researchers to propose a phase-field model for ductile fracture, where the evolution of the phase-field is coupled to the evolution of plastic strains in the body, first under the assumption of small deformations, and then for finite deformations.
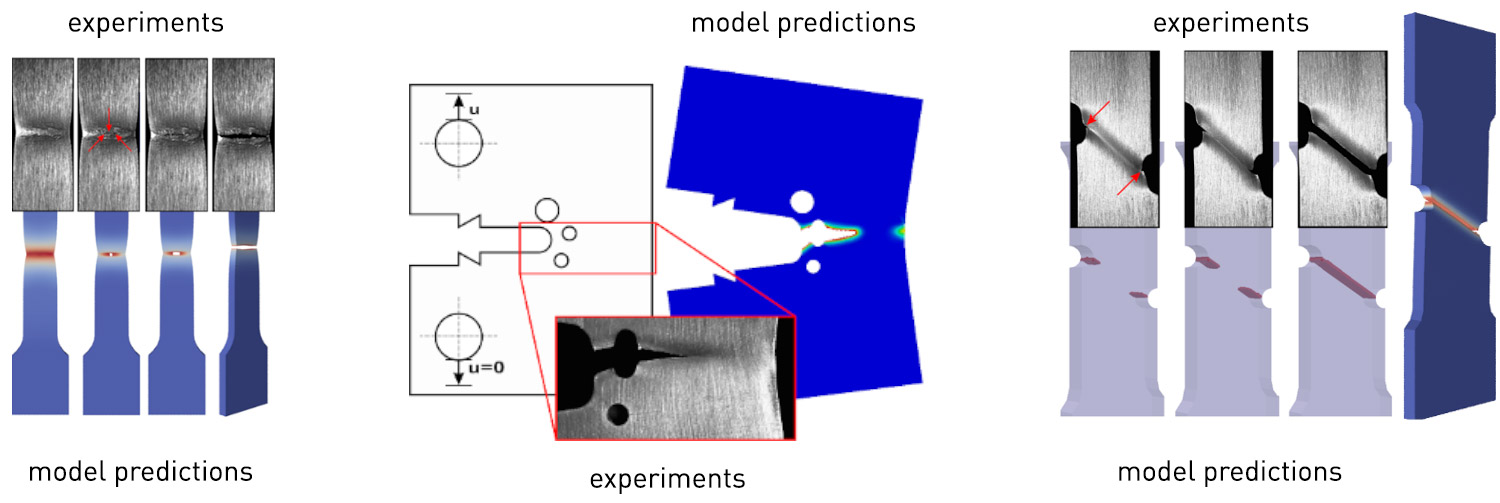
The model was shown to be able to reproduce a number of behavioural features typical of ductile fracture, as seen in experiments taken from the literature as well as in our own experiments. Among these are the observed sequence of elasto-plastic deformation, necking and fracture in flat specimens; the occurrence of cup-cone fracture patterns in axisymmetric specimens; the role played by notches and by their size on the measured displacement at fracture; and the sequence of distinct cracking events observed in more complex specimens.
Also, in collaborations with our colleagues at external page CERECAM, we developed a model for fracture in single crystal plasticity. More recently, as several other phase-field ductile fracture models had been proposed in the meantime and within a collaboration with the external page Università La Sapienza in Rome, we carried out a comparative study of phase-field models for ductile fracture which can be a good starting point to approach the subject. An efficient adaptive isogeometric discretization scheme for our ductile fracture model was recently devised in collaboration with our colleagues of the external page TU Dresden and is illustrated here.
Funding:
external page ERC Starting Researcher Grant “Mechanical modeling of interfaces in advanced materials and structures” (2011-2016).
external page MIUR-external page DAAD Joint Mobility Program “Variational approach to fatigue phenomena with phase-field models: modeling, numerics and experiments” (2016-2017).