Computational aspects
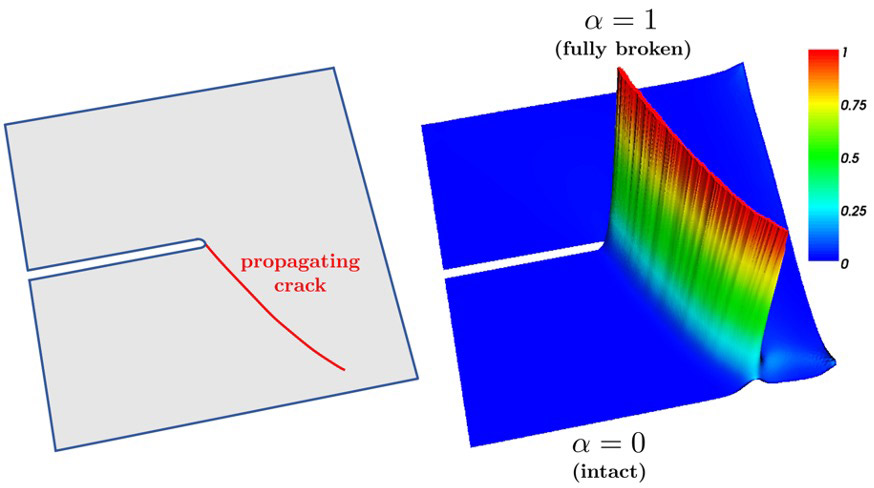
In the phase-field approach to fracture, a sharp crack is approximated through the continuous but steep variation of an order parameter (the crack phase field).
Compared to the alternative tools of computational fracture mechanics, this approach has the major advantage of not needing any explicit or implicit tracking of discontinuities. Any arbitrarily complicated “crack” pattern is recovered from the solution of partial differential equations; the finite element discretization of these equations can use any type of mesh and the extension from two to three dimensions is straightforward. However, when it comes to computing, some challenges arise.

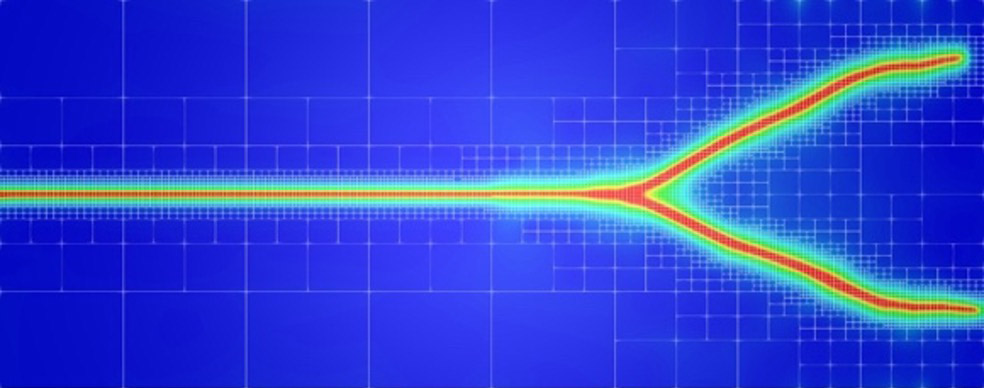
The non-convexity of the energy functional whose minimization delivers the governing equations of the approach leads to the need for special care while devising solution strategies. We developed a specially tailored line search procedure that enables the efficient monolithic solution of the governing equations. Non-convexity also leads to possible non-unique solutions.
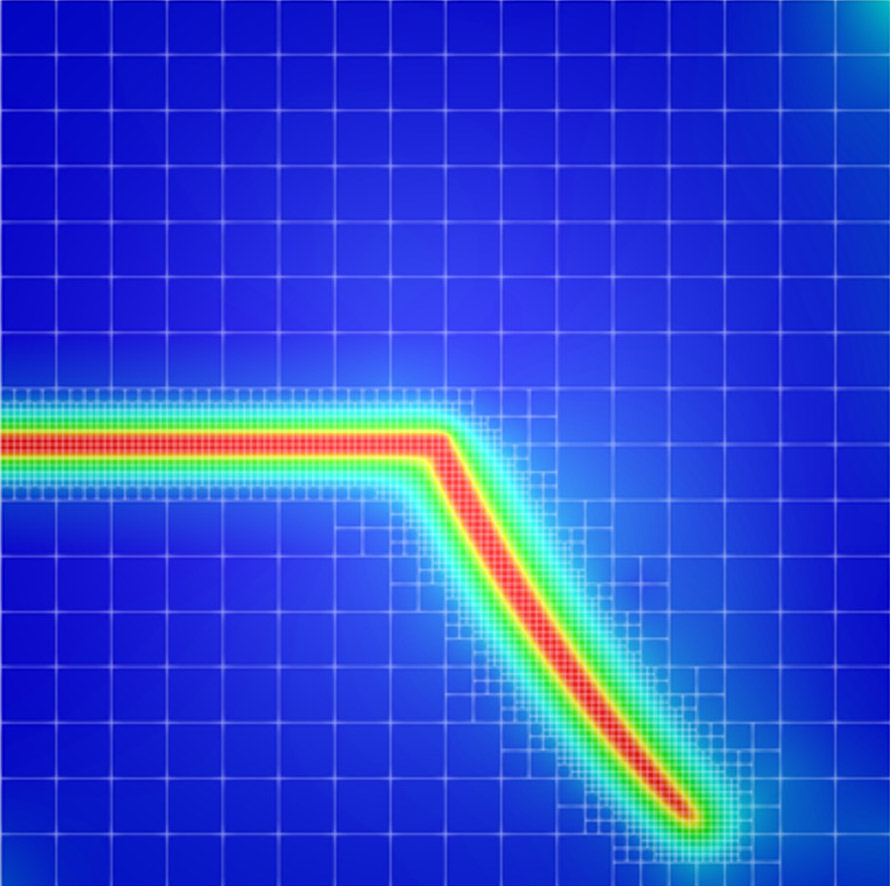
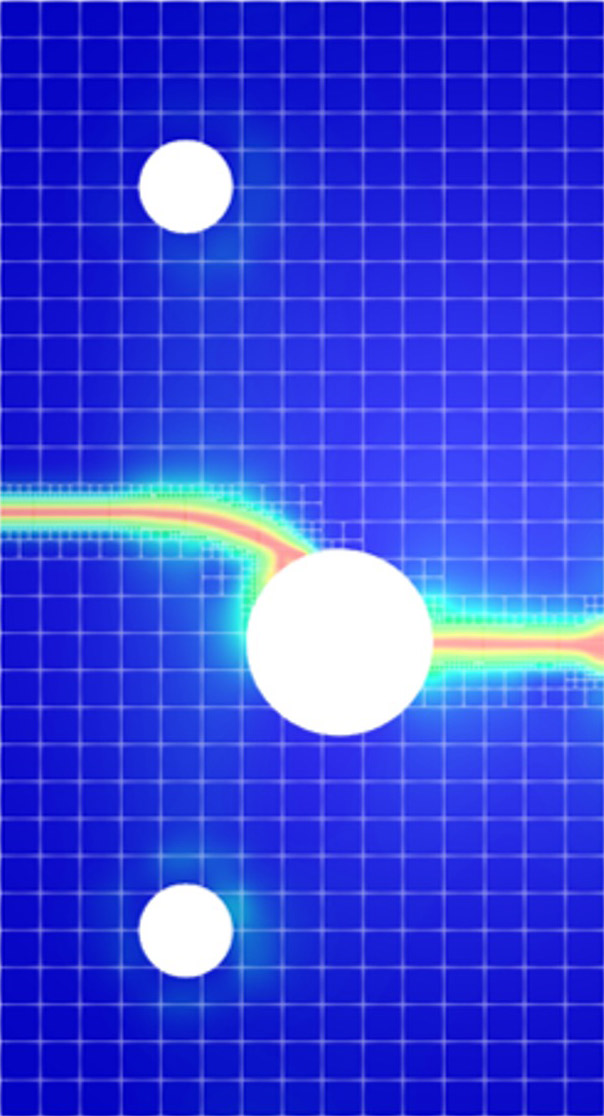
The width of the smeared approximation of the crack is proportional to a length scale parameter. The smaller this parameter, the closer the smeared approximation approaches the sharp crack limit. On the other hand, a very small parameter implies the need for a very fine finite element mesh to resolve the steep variation of the crack phase field. In collaboration with our colleagues at the external page Technische Universität München we discretized the governing equations of the phase-field fracture model with a multi-level hp-FEM scheme leading to high efficiency. We also solved the problem within the framework of the finite cell method, which is useful to mesh complex geometries for industrial applications.
The crack phase-field, when interpreted as a damage variable, should not decrease over time, which is referred to as the irreversibility constraint. We developed a simple penalty method to enforce this constraint, supplemented by a practical and accurate estimation bound for the penalty parameter.
Funding:
external page ERC Starting Researcher Grant “Mechanical modeling of interfaces in advanced materials and structures” (2011-2016).
external page DFG Project “Phase-field computation of brittle fracture: robustness, efficiency, and characterisation of solution non-uniqueness” (2018-2019).