Simulation of extrusion-based processes: Floating Isogeometric Analysis
Extrusion-based Additive Manufacturing (AM) is a prominent candidate for advanced and customized fabrication in which tempered feedstock is forced through an extrusion nozzle. Controlled deposition in strand-by-strand/layer-by-layer fashion and subsequent solidification form the final part. Amongst the most widely employed printing materials are polymers, which exhibit a combination of solid- and fluid-like behavior. The complexity of the AM process has motivated the development and application of simulative computer tools to support progress in this field of technology. These tools study carefully chosen mathematical models which depict the real AM process.
Solving such Initial-Boundary-Value-Problems is particularly challenging, as the solution depends on the history of extreme deformations experienced by the simulated printing material. In this context, techniques of Computational-Solid-Mechanics as Lagrangian FEA and Isogeometric Analysis (IGA) face trouble with excessive mesh-distortion. Employing instead a static Eulerian mesh, CFD techniques can remedy this issue only at the cost of additional efforts to track moving boundaries and introduction of nonlinear advective terms. Meshless methods have settled in-between and update basis functions only as far analysis-suitable shape is preserved, demanding the abolishment of the rigid mesh division. Though mesh-distortion is naturally circumvented, the abdication of a mesh often compromises the mathematical properties of such alternative basis functions.
Against this background, we develop Floating Isogeometric Analysis (FLIGA) which emerges from the transfer of meshless core concepts to mesh-based IGA. This novel approach resolves the mesh-distortion problem along one curved direction of the physical mesh, which we term the characteristic direction. At the same time the approach maintains the favorable mathematical background of B-Splines. To this end, the classical tensor-product structure of multivariate B-Splines is modified, allowing chains of basis functions to unidirectionally float against one another on the parametric domain.

When adapted to the deformations along the characteristic extrusion axis in AM processes, the floating of basis functions on the parametric domain can preserve their analysis-suitable shape after the final map to physical space, resembling the meshless paradigm. Though the global element division is given up, such division persists on the level of single basis functions, each being still a conventional multivariate B-Spline.
B-Spline bases computed from this floating tensor-product structure preserve many properties of classical B-Spline bases with positive effect on the analysis, such as partition of unity, first-order consistency or weak Kronecker-delta property. Additionally, moving boundaries are naturally handled within FLIGA, while avoiding classical remeshing. Evaluating Floating Tensor-Product B-Splines with a material point integration scheme makes FLIGA a promising tool for AM simulation capable to handle viscoelasticity and solidification.
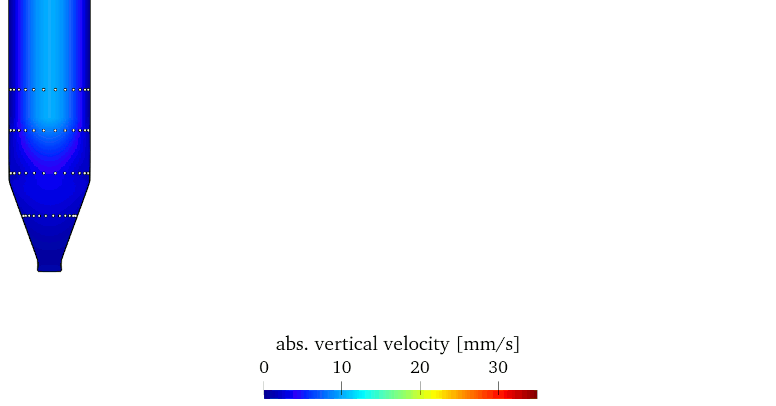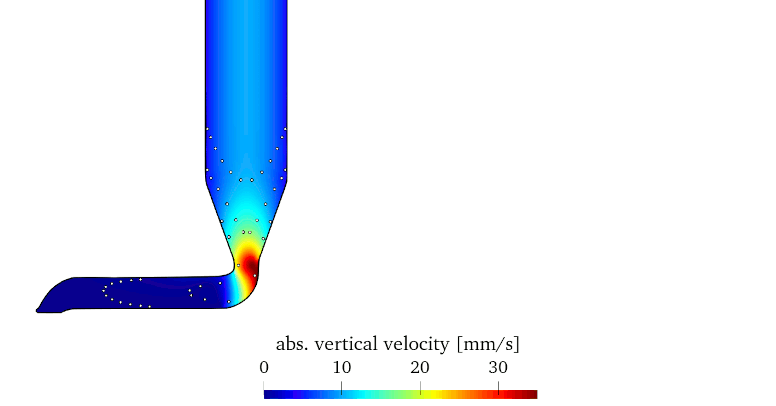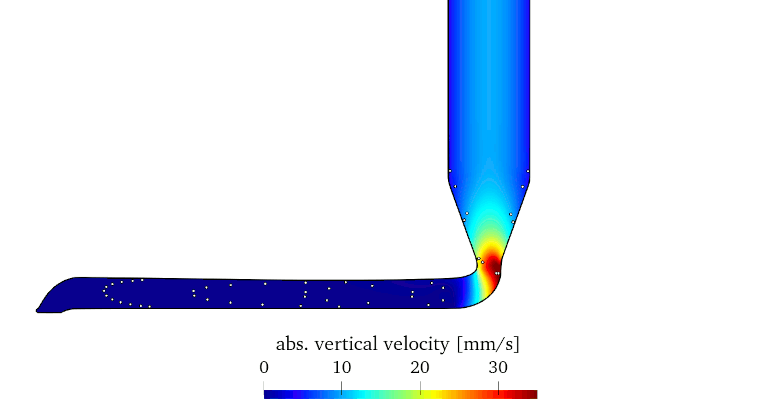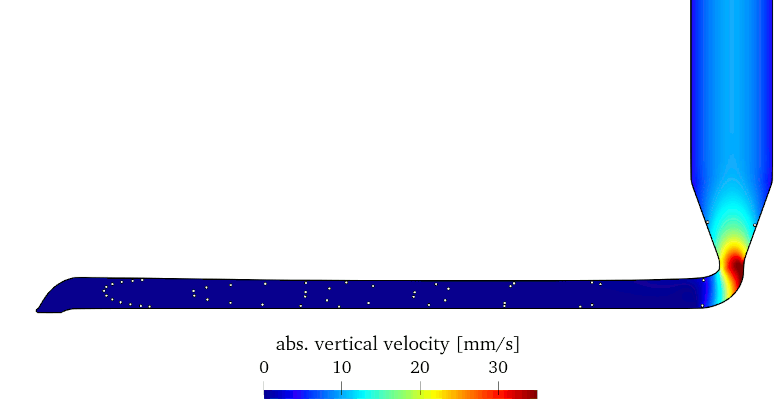
Current activities include a numerical study of the AM process with FLIGA including comparison to experiments. Methodical enhancements are also an ongoing field of research.